MENGAJAR STRUKTUR MATEMATIKA: BRUNER DAN REPRESENTASI KOGNITIF KONSEP-KONSEP MATEMATIS (BAG IV)

G.    BAHASA GAMBAR DALAM PROBLEM SOLVING

Pada semua jenjang pendidikan mulai dari Sekolah Dasar, Sekolah Lanjutan, dan Perguruan Tinggi, masalah utama dalam mengajarkan problem solving terletak pada meyakinkan siswa untuk mencatat detil masalah di kertas jawaban. Siswa yang mencatat informasi-informasi yang berhubungan dengan masalah dapat menjadi pemecah masalah yang sukses.

Beberapa siswa yang tidak bersedia menulis detil di kertas jawabannya bisa saja karena menolak persyaratan tertentu dimana informasi disajikan dalam masalah kata harus diterjemahkan ke dalam ekspresi numeris. Simbol-simbol dan grammar matematika merupakan bahasa yang tidak familiar bagi siswa, dan siswa mempunyai kecepatan dan kecakapan yang berbeda  untuk memahaminya. Ketika bahasa ekspresi bilangan tidak familiar, siswa harus bekerja keras mengekspresikan pemahamannya terhadap masalah dalam bahasa asing, daripada berkonsentrasi terhadap masalah itu sendiri.

Pendekatan alternatif di awal mengajar problem solving adalah dengan menyediakan bahasa  gambar (pictorial language) dimana siswa dapat mencatat informasi. Dalam pengalaman penulis, bahasa mendorong siswa untuk menulis informasi di kertas jawaban. Selanjutnya, mereka akan mencatat informasi dengan cara yang bagi mereka berguna. Dengan membangkitkan perilaku pemrosesan informasi dengan baik secara perlahan pada tingkat primer, kita dapat menyajikan masalah yang rumit secara bertahap dan memperkenalkan bahasa simbolik untuk dikembangkan siswa.

Berikut ini akan digambarkan dua contoh penggunaan bahasa gambar siswa dalam problem solving (Schneider, 1980). Pada contoh pertama, masalah adalah bagian dari kurikulum jenjang pendidikan pertama atau kelas satu (Comprehensive School Mathematics Program 1978a). Siswa menggunakan titik, anak panah, dan rangkaian untuk menyajikan hubungan numeris dari pernyataan masalah. Pada contoh yang kedua, masalah adalah bagian dari kurikulum jenjang pendidikan kelima atau kelas lima (Comprehensive School Mathematics Program 1978b), bahasa diperkaya dengan memberikan interpretasi geometri berupa titik dan anak panah.

1.      Bahasa gambar di kelas satu

Awalnya di kelas satu ini, siswa menjadi familiar menggunakan titik, anak panah, dan rangkaian dalam menceritakan cerita. Sebagai contoh, guru yang menggambar rangkaian 2 warna yang berbeda, masing masing disertai dengan titik. Titik pada rangkaian sebelah kiri merepresentasikan apel dan rangkaian di sebelah kanan merepresentasikan kuda. Setelah bertanya kepada siswa jumlah apel dan kuda, kemudian guru menggambar anak panah yang berwarna untuk menunjukkan apel-apel mana yang dimakan kuda tertentu. (gambar 4). Diskusi berpusat pada kuda mana yang makan apel paling banyak, berapa banyak kuda yang tidak makan apel, dan sebagainya.

Dalam pelajaran yang lain, siswa menemukan cerita yang sesuai dengan gambar 5 berikut. Interpretasi berikut adalah jawaban siswa: anak-anak di dalam rangkaian dan hewan kesayangan di luar, dengan anak panah untuk menunjukkan ”hewan ini adalah kesayanganku”; atau anjing di dalam dan tulang di luar rangkaian dengan anak panah menunjukkan ”mengunyah”. Sepanjang tahun anak berpengalaman dengan banyak masalah dari tipe ini.

Selama semester kedua, siswa diberi tiga masalah dengan interval waktu 2 minggu. Guru membacakan setiap masalah dengan keras sebanyak dua kali, kemudian siswa bekerja secara individu dengan menggunakan kertas dan pensil warna untuk menggambar apapun yang dipikirkan yang dapat membantu mereka menyelesaikan masalah.

a.             Seorang temanku mempunyai SPBU (pom bensin). Pagi ini 7 buah mobil datang dan setiap mobil membutuhkan 4 ban baru. Berapa banyak ban yang di jual temanku?

b.            Enam gurita pergi ke toko sepatu dan mereka semua membutuhkan sepatu baru. Berapa banyak sepatu yang dibutuhkan bersamaan?

c.             Ibu mempunyai soda sebanyak 24 botol dan akan ditempatkan pada dus yang hanya memuat 8 botol, berapa banyak dus yang diperlukan?

Masalah-masalah tersebut terlihat sangat tingkat tinggi bagi siswa kelas satu, namun penggunaan titik, rangkaian, dan anak panah membantu siswa menyelesaikan masalah tersebut. Kebanyakan siswa mengerjakan masalah pertama, sekitar dan jumlah siswa yang mampu menyelesaikan masalah dua dan tiga. Beberapa di antaranya gagal mencari jawaban yang benar pada masalah kedua dan menjawab 49 dan 46, menunjukkan kesalahan menghitung. Gambar 5-7 menunjukkan gambar pekerjaan yang dilakukan siswa untuk menyelesaikan masalah dengan menggunakan titik, rangkaian, dan anak panah.

Untuk menyelesaikan masalah 1, Chris menggambar 7 buah titik besar untuk mrepresentasikan mobil dan 4 buah titik kecil untuk merepresentasikan ban mobil. Anak panah menunjukkan ban untuk suatu mobil (gambar 6).

Untuk menyelesaikan masalah 2, Meredith menggambar rangkaian untuk setiap gurita dan menempatkan delapan titik sebagai sepatu, di dalam rangkaian. Terlihat bahwa dia menggambar terlalu banyak rangkaian, sehingga dia mencoret 2 rangkaian di antaranya (gambar 7). Untuk masalah 3, Shannon menggambar titik untuk botol soda dan rangkaian untuk dus yang berisi 8 (Gambar 8).

Langkah selanjutnya, siswa menghitung.  Setelah selesai menghitung, siswa membisikkan jawaban kepada guru dan siswa yang telah selesai terlebih dahulu diminta untuk menuliskan cerita bilangannya. Hal ini karena kebanyakan siswa kelas satu tidak tahu fakta perkalian atau pembagian yang muncul di dalam masalah, sehingga mereka diminta menuliskan cerita bilangannya (kalimat), tanpa bantuan gambar yang mereka buat. Demikian pengalaman-pengalaman yang ditunjukkan siswa kelas satu yang dapat menggunakan bahasa gambar untuk menyatakan detil masalah. Dengan mencatat secara detil, mereka dapat berkonsentrasi dalam menghitung atau aritmatika.

1.      Bahasa Gambar di Kelas Lima

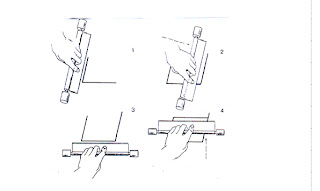
Geometri selalu menyediakan latar yang membantu untuk menyelesaikan masalah aritmatika. Sekelompok siswa kelas lima sedang mengeksplorasi jajargenjang. Menggunakan suatu alat yaitu translator (Gambar 9), mereka belajar mengkonstruksi jajargenjang dan membentuk beragam konstruksi berdasarkan jajargenjang tersebut, beberapa digambarkan di gambar 10.

 Gambar 9

Gambar 10

Siswa di kelas belajar dengan menggunakan buah-buahan pasar yang dibedakan 2 jenis yaitu apel dan arbei. Sebuah pasar kecil menjalin relasi antara pemilik dengan konsumen yang ditunjukkan dengan adanya aturan untuk membolehkan adanya pengembalian dan penukaran apel dan arbei. Siswa mengembangkan teknik mencatat transaksi pada pola-pola geometris. Pada gambar 11, anak panah merah merepresentasikan pembelian 1 kg apel dan anak panah biru menunjukkan pembelian 1 kg arbei. Setiap titik merepresentasikan hasil pembelian tertentu:”1a” untuk 1 kg apel, ”1b” untuk satu kg arbei, ”3a + 2b” untuk 3 kg apel dan 2 kg arbei, dsb. Tentu saja pembelian yang mungkin adalah untuk yang bukan dalam bentuk seperti 0.5a, 3.25 a + 1.50b, dsb.

Ketika siswa menjadi lebih familiar dengan alat seperti gambar di atas, mereka menggunakannya untuk merepresentasikan hasil penuh transaksi. Paula mengkonstruksi sumbu apel dan sumbu arbei (gambar 12). Titik merepresentasikan 1 kg apel dan 1 kg arbei. Menggunakan translator, Paula mengkonstruksi jajargenjang untuk menempatkan titik untuk merepresentasikan beberapa transaksi tambahan. (catatan: ”” adalah notasi yang digunakan yang identik dengan ”-1”)

Penghitungan harga adalah kesulitan selanjutnya. Guru memberikan informasi harga apel dan arbei, kelas menghitung biaya beberapa transaksi. Pola-pola geometris melibatkan mental aritmatika. Contohnya, untuk membantu harga 2 kg apel dan 3 kg arbei, seorang anak melangkah dari titik 0 ke 2a + 3b, menambahkan biaya tiap kg setiap langkahnya. Untuk menemukan biaya kuantitas non bulat, siswa bergantung pada pemahaman yang telah dikenalnya tentang konsep garis bilangan.

Perhatikan 2 masalah berikut ini.

Masalah :  Harga 1 kg apel 30 sen, dan harga 1 kg arbei 40 sen. Berapa banyak yang dapat dibeli jika hanya punya uang 1 dolar?

Masalah :   cari solusi persamaan berikut, 30x + 40y = 100

Tentu saja kedua masalah ini adalah sama. Masalah pertama akan lebih diminati siswa karena konteksnya pasar. Untuk menyelesaikan masalah 1, Jenny mengkonstruksi pola-pola dan titik berwarna merah merepresentasikan pembelian 1 dolar (gambar 13).

Setelah beberapa titik penyelesaian ditemukan, beberapa siswa menebak bahwa semua titik berada pada garis yang sama. Dalam mengetes dugaan mereka, siswa menghitung biaya transaksi yang direpresentasikan titik yang lain di garis. Memilih titik pembelian, siswa memproyeksikannya sejajar  sumbu y (arbei) pada sumbu x (apel) dan sebaliknya (gambar 14). Proyeksi pada sumbu x menunjukkan jumlah apel yang dibeli, proyeksi pada sumbu y (arbei) menunjukkan jumlah arbei yang dibeli. Berbekal informasi ini, anak mengecek biaya pembelian. 

Dalam meneliti masalah, siswa memikirkan transaksi dengan 60 sen dan transaksi tanpa uang. Sebagai contoh, dengan harga 1 kg apel 20 sen dan harga 1 kg arbei 30 sen, 3 kg apel dapat dibeli setara dengan 2 kg arbei. Kita dapat merepresentasikan dengan  dan jika disajikan alam bentuk uang adalah .

Setelah menempatkan titik pada beragam transaksi, Vonda membedakan 2 garis pada pola yang dibuatnya (gambar 15). Dua garis tersebut sejajar, menurut dugaan siswa, dan disimpulkan dengan percobaan menggunakan translator.Tentu saja garis-garis tidak dapat disilangkan, selanjutnya hanya ada transaksi dengan 2 harga.

         Dalam mengkonstruksi pola, siswa menyukai kebebasan menentukan lay-out. Pada saat yang sama, mereka dapat mengkonstruksi gambar dengan tepat menggunakan translator. Siswa berhati-hati dalam mengkonstruksi model geometri pada situasi pasar akan menghasilkan tingkat partisipasi yang tinggi daripada jika guru menyediakan pola atau menggunakan pendekatan aritmatika murni. Faktanya, ada interaksi geometri dengan aritmatika dengan menampilkan penyelesaian masalah di atas. Selanjutnya, display itu sendiri menyarankan adanya penyelesaian tambahan.

 

Dalam kedua situasi, bahasa gambar mendorong siswa menyelesaikan masalah dan menyediakan alat yang bermanfaat untuk mengekspresikan informasi. Banyak siswa kelas satu yang mampu bergerak dari representasi gambar ke ekspresi numeris. Siswa kelas lima diajarkan mengamati dan menyimpulkan secara implisit pernyataan masalah melalui penggunaan geometri. Baik sebagai jembatan bahasa numeris atau sebagai konteks yang kaya untuk mengeksplorasi masalah, bahasa gambar terbukti berhasil menjadi alat untuk menyelesaikan masalah.

DAFTAR PUSTAKA

Schneider, Joel. Kevin W. Saunders. 1980. Pictorial Languages in Problem Solving. In Krulik, Stephen., Robert E Reys. Problem Solving in School Mathematics. National  Council of Teachers of Mathematics